| Ошибка? |
 |
| Радио онлайн |  |
| Магнитные бури |

|
| Онлайн |
Онлайн всего: 1 Гостей: 1 Пользователей: 0 |
|
В категории материалов: 12
Показано материалов: 1-10 |
Страницы: 1 2 » |
Сортировать по:
Дате ·
Названию ·
Рейтингу ·
Комментариям ·
Просмотрам
 Волновое преобразование (wavelet) - новый перспективный метод цифрой обработки сигналов. Основные области использования для цифровой обработки ЭКГ: анализ (исследование вариабельности сердечного ритма, ЭКГ высокого разрешения, выделение QRS) и сжатие сигнала ЭКГ с минимальными потерями (рис.12). Преимущество волнового преобразования заключается в способности выделить детали ЭКГ с наилучшим локальным разрешением по частоте... Волновое преобразование (wavelet) - новый перспективный метод цифрой обработки сигналов. Основные области использования для цифровой обработки ЭКГ: анализ (исследование вариабельности сердечного ритма, ЭКГ высокого разрешения, выделение QRS) и сжатие сигнала ЭКГ с минимальными потерями (рис.12). Преимущество волнового преобразования заключается в способности выделить детали ЭКГ с наилучшим локальным разрешением по частоте...
|
 We introduce the concept of penalized wavelets to facilitate seamless embedding of wavelets into semiparametric regression models. In particular, we show that penalized wavelets are analogous to penalized splines; the latter being the established approach to function estimation in semiparametric regression. They differ only in the type of penalization that is appropriate. This fact is not borne out by the existing wavelet literature, where the regression modelling and fitting issues are overshadowed by computational issues such as efficiency gains afforded... |
 Исследуем последовательность длительностей правления магистров при помощи комплексного вейвлет-преобразования. Идея этого метода заключается в свёртке исследуемого сигнала с финитной базисной функцией ψ(t), моделирующей уединённую комплекснозначную волну, называемой вейвлетом (всплеском) и в последующем изучении полученного интегрального преобразования исходной функции. Мы попадаем в один специальный случай операционного исчисления, изобретённый Ингрид Добечи. Популярному введению в эту теорию посвящён восьмой номер "Компьютерры" за 1998 г., смотри... |
 В буквальном переводе с английского языка слово wavelet означает маленькая волна, такое название объясняется формой функций,используемых в вейвлет-анализе. Термин вейвлет-анализ по смыслу аналогичентермину Фурье-анализ. В обоих случаях речь идет о представлении исследуемогопроцесса в виде линейной комбинации различных функций, именуемых базисомсоответствующего преобразования. Для вейвлет - анализа характерно понятиемасштаб ( В буквальном переводе с английского языка слово wavelet означает маленькая волна, такое название объясняется формой функций,используемых в вейвлет-анализе. Термин вейвлет-анализ по смыслу аналогичентермину Фурье-анализ. В обоих случаях речь идет о представлении исследуемогопроцесса в виде линейной комбинации различных функций, именуемых базисомсоответствующего преобразования. Для вейвлет - анализа характерно понятиемасштаб (scale), даже графическое представление ввиде диаграммы специального... |
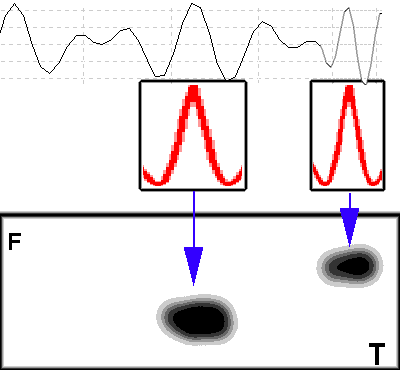 Вэйвлеты (wavelet) и вэйвлет-преобразование - это новый способ обработки и исследования сигналов, теория которого разработана совсем недавно, с появлением быстродействующих компьютеров, так как требует большого объема вычислений. Вэйвлет можно считать трехмерным спектром, где по оси X - время, по оси Y - частота, а по оси Z - амплитуда гармоники с данной частотой в данный момент времени. Обычно на двухмерной плоскости (на экране, на бумаге) ось Z отображают в виде градаций черного цвета. При этом черный цвет - максимальная амплитуда, а белый - минимальная. Тогда самые интересные места сразу видно по черным пятнам. |
 Однажды папа показал мне созданную им аналоговую цветомузыку. Три прожектора весело мигали четко под музыку, каждый настроен на свой диапазон частот, и четвертый прожектор загорался только тогда, когда какой-либо из прожекторов погасал, чтобы в комнате не было темно в затишье. Потом что-то в ней сломалось, и лежала она пылилась добрый десяток лет на полке. Поскольку я очень люблю слушать музыку... |
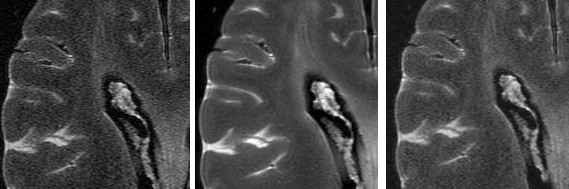 Новые эффективные способы обработки изображений стали возможны с развитием теории вейвлетов, которые по сравнению с преобразованием Фурье позволяют с гораздо большей точностью представлять мельчайшие особенности функций, изображений и сигналов, вплоть до разрывов первого рода (скачков)... Новые эффективные способы обработки изображений стали возможны с развитием теории вейвлетов, которые по сравнению с преобразованием Фурье позволяют с гораздо большей точностью представлять мельчайшие особенности функций, изображений и сигналов, вплоть до разрывов первого рода (скачков)... |
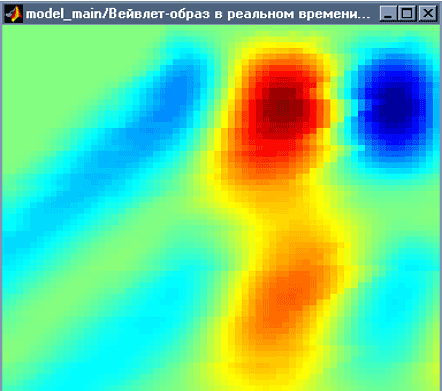 Статья посвящена реализации модели вейвлет-преобразователя, работающего в режиме квазиреального времени, в дальнейшем, квазиреального во времени вейвлет-преобразователя, а также возможности его использования для анализа сигналов к которым неприменимо классическое Фурье преобразование. Модель реализована с использованием программных продуктов MATLAB... |
|
Стандартные методы спектрального оценивания с использованием быстрого вычислительного алгоритма, именуемого быстрое преобразование Фурье (БПФ), основаны на модели представления данных с помощью рядов Фурье, то есть анализируемый процесс полагается состоящим из некоторого набора гармонически связанных синусоид. В нетехнических областях в течении многих лет используются модели на основе других временных рядов. Юл и Уокер использовали АР-модели для прогнозирования трендов во временных рядах, характеризующих экономические данные. Прони предложил процедуру согласования экспоненциальных моделей с данными экспериментов в области химии газов. Ряд других моделей появился в других областях, связанных со статистическим и численным анализом...
|
|
Вейвлет-преобразование является инструментом кратномасштабного анализа: с его помощью сигнал представляется в виде некоторой аппроксимации и набора деталей, отличающих данную аппроксимацию от исходного сигнала. Такое представление позволяет "отсеять" незначительные изменения сигнала, сосредоточившись на изучении его глобальных особенностей, либо, напротив, рассмотреть его "мелкие детали", неразличимые на фоне "крупномасштабных" изменений...
|
|


