Волновое преобразование (wavelet) - новый перспективный метод цифрой обработки сигналов. Основные области использования для цифровой обработки ЭКГ: анализ (исследование вариабельности сердечного ритма, ЭКГ высокого разрешения, выделение QRS) и сжатие сигнала ЭКГ с минимальными потерями (рис.12).
Преимущество волнового преобразования заключается в способности выделить детали ЭКГ с наилучшим локальным разрешением по частоте. Ортогональное волновое преобразование эффективно сжимает ЭКГ (например, в 6 раз при погрешности 2%).
Метод позволяет выявить в частотной области ненормальные потенциалы внутри QRS, удлиненный QT сегмент, исследовать P и T волны, а также QT и ST. Представлены результаты его применения для исследования изменения спектральных компонентов (до 0.4 Гц) ритма во времени.

 Рис.1. Вейвлет-преобразование кардиоинтервалограммы.
Волновое преобразование - эффективный метод для исследования вариабельности сердечного ритма. В настоящее время этот метод только начинает внедряться и требуется его исследование для широкого клинического применения.


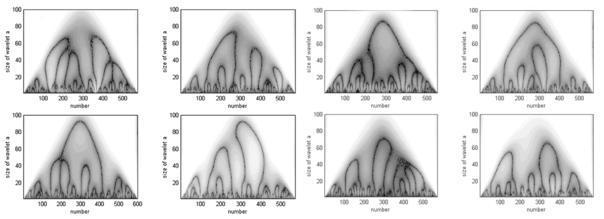
 Рис.2. Вейвлет-преобразование кардиоинтервалограмм.

На рис.2 представлены типичные формы вейвлет-преобразования для кардиоинтервалограмм. Следует отметить, что изображенные результаты вейвлет-преобразования имеют четкую древовидную структуру. Это позволяет выявлять структуру интервалограммы и использовать ее в качестве одного из критериев диагностики. Дальнейшее развитие метода и оценка перспектив его предусматривается на втором этапе работ.
 В процессе выполнения работы было написано специальное программное обеспечение, реализующее обработку по данному методу. Программное обеспечение оформлено в виде стандартизованного программного модуля для разрабатываемой автоматизированной диагностической системы.

Литература 

Анохин П.К. Системные механизмы высшей нервной деятельности. М.: Наука, 1979. 453 с.
Ахромеева Т.С., Курдюмов С.П., Малинецкий Г.Г., Самарский А.А. Нестационарные структуры и диффузионный хаос. М.: Наука, 1992.
Воронин Л.Г. Эволюция высшей нервной деятельности. М.: Наука, 1977, 128 с.
Гаазе-Раппопорт М.Г., Поспелов Д.А. От амебы до робота: модели поведения. М.: Наука, 1987. 288 с.
Гленсдорф П., Пригожин И. Термодинамическая теория структуры, устойчивости и флуктуаций. М.: Мир, 1973.
Данилов Ю.А. Роль и место синергетики в современной науке. http://www.iph.ras.ru/~mifs/dan2.htm.
Данилов Ю.А., Кадомцев Б.Б. Что такое синергетика? http://www.iph.ras.ru/~mifs/dan.htm.
Е.Федер, Фракталы, М., МИР, 1991
Кауффман С. Антихаос и приспособление // В мире науки. 1991. N.10. С. 58-65.
Компьютеры и нелинейные явления. М.: Наука, 1988.
Компьютеры, модели, вычислительный эксперимент. М.: Наука, 1988.
Корогодин В.И. Информация и феномен жизни. Пущино, 1991, 202 с.
Короновский А.А., Трубецков Д.И. Нелинейная динамика в действии: как идеи нелинейной динамики проникают в экологию, экономику и социальные науки. Саратов: ГосУНЦ "Колледж", 1995.
Левкович-Маслюк, Дайджест вейвлет-анализа, Компьютерра, №8,1998.
Малинецкий Г.Г. Хаос, структуры, вычислительный эксперимент. М.: Наука, 1997.
Малинецкий Г.Г., Рузмайкин А.А., Самарский А.А. Модель долговременных вариаций солнечной активности. Препринт ИПМ АН СССР, 1986, N170.
Манделъштам Л. И. Лекции по колебаниям. М.: Изд-во АН СССР, 1955. 503 с.
Математические проблемы в биологии: Сб. статей. М.: Мир, 1962, с. 258.
Николае Г., Пригожин И. Самоорганизация в неравновесных системах. М.: Мир, 1979. 512 с.
Новое в синергетике. Загадки мира неравновесных структур. М.: Наука, 1996.
Р.М. Баевский, О.И. Кириллов, С.З. Клецкин, Математический анализ изменений сердечного ритма при стрессе 1984.
Романовский Ю. М., Степанова Н. В., Чернавский Ц. С. Математическое моделирование в биологии. М.: Наука, 1975. 343 с.
Самарский А.А., Галактионов В.А., Курдюмов С.П., Михайлов А.П. Режимы с обострением в задачах для квазилинейных параболических уравнений. М.: Наука, 1987.
Самарский А.А., Михайлов А.П. Математическое моделирование. М.: Наука, 1997.
Фракталы в физике. М.: Мир, 1988.
Френкель А., Бар-Хиллел И. Основания теории множеств. М.: Мир, 1966. 556 с.
Хакен Г. Синергетика. М.: Мир, 1980.
Хоффман У. Система аксиом математической биологии.- В кн.: Кибернетический сборник. М.: Мир, 1975, вып. 12, с. 184-207.
Цетлин М.Л. Исследования по теории автоматов и моделирование биологических систем. М.: Наука, 1969. 316 с.
Эбелинг В. Образование структур при необратимых процессах. М.: Мир, 1979, с. 13-14.
Эйген М., Винклер Р. Игра жизнь. М.: Наука, 1979, с. 53.
Эйген М., Шустер П. Гиперцикл. Принципы самоорганизации макромолекул. М.: Мир, 1982. 270 с.
Nonlinear partial differential equations. N. Y.: Acad. press, 1967, p. 223.
C. D. Haagensen, Diseases of the Breast, Third Edition, Saunders Company, 1986.
Choaos and order in nature /Ed. by H.Haken. B. etc. 1980. 271 p.
Dynamic of synergetic systems/ Ed. by H. Haken. В. etc., 1980. 271 p.
F. Yang, W. Liao, Modeling and Decomposition of HRV Signals with Wavelet Transforms, IEEE Engineering in Medicine and Biology, 1997, Vol. 16, No. 4, pp. 17-22.
Feistel R. On the evolution of biological macromolecules. Precelular organization. 4. Holobiotic competition // Studia biophysica. 1983. V.93. N.2. P. 113-128.
Fraser A.M., Swinney H.L. Independent coordinates for strange attractors from mutual information// Phys. Rev. A. 1986. V.33. N2, p.1131-1140.
M. Akay, Wavelet Applications in Medicine, IEEE Spectrum, 1997, Vol. 34, No. 5, pp. 50-56.
M. Antonini, M. Barlaud, P. Mathieu, I. Daubechies, Image Coding Using Wavelet Transform, IEEE Transanctions on Image Processing, 1992, Vol.1, No. 2, рр. 205-220.
Mandelbrot B.B. Fractals: form chance and dimension. San Francisco.: Freeman Comp. 1977.
P. C. Ivanov, M. G. Rosenblum, C. K. Peng, J. Mietus, S. Havlin, H. E. Stanley, A. L. Goldberger, Scaling Behaviour of Heartbeat Intervals Obtained by Wavelet - Based Time - Series Analysis ", Nature, 1996, Vol. 383, No. 26, pp. 323-327.
S. Blanco, S. Kochen, O. A. Rosso, P. Saldado, Applying Tome-Frequency Analysis to Seizure EEG Activity, IEEE Engineering in Medicine and Biology, 1997, Vol. 16, No. 1, pp. 64-71.