Статья посвящена реализации модели вейвлет-преобразователя, работающего в режиме квазиреального времени, в дальнейшем, квазиреального во времени вейвлет-преобразователя, а также возможности его использования для анализа сигналов к которым неприменимо классическое Фурье преобразование. Модель реализована с использованием программных продуктов MATLAB v6.0 и поставляемой в составе системы MATLAB системы визуального моделирования Simulink v4.0.
Базис модели.
Как известно, вейвлет-преобразование хорошо локализовано как по времени, так и по частоте, что позволяет отслеживать изменение сигнала во времени, то есть позволяет оперировать "мгновенной частотой". Модель построена по принципу "исходный сигнал - чёрный ящик - сигнал на выходе" (рис 1) с реализацией в "черном ящике" нижеописанного алгоритма вейвлет-преобразования.
 Рис.1 Прохождение сигнала через вейвлет-преобразователь (черный ящик)
Пусть имеется некоторый произвольный сигнал - некоторая функция f(x), над которой с помощью вейвлета ψ произведем вейвлет-преобразование. Допуская, что здесь и далее переменная x соответствует времени, в результате такого преобразования будем иметь функцию Wf(x,a), зависящую от двух переменных - от времени x и от масштаба a. Процедура вычисления значения Wf(x,a) для каждой пары x и a (a>0) в этом случае будет включать:
- Растяжение вейвлета ψ в a раз по горизонтали и в 1/√a раз по вертикали.
- Сдвиг вейвлета в точку x, обозначив полученный вейвлет как ψx,a.
- "Усреднение" значения сигнала в окрестности точки a при помощи ψx,a.
Определяя цвет каждой точки для всех пар (x,a) в зависимости от абсолютной величины суммы, функция Wf(x,a) будет представлять собой не что иное, как вейвлет-образ преобразуемого сигнала.
Строго это выглядит следующим образом [1-3]:
Описание модели.
На рис.2 представлена обобщенная модель вейвлет-преобразователя отвечающего рис. 1 с блоком генератора сигнала, блоками отображения вейвлет-образа и коэффициентов вейвлет-преобразования, а также блоком записи значений сигнала, подключенными, соответственно, к входу и двум выходам преобразователя.
 Рис.2 Обобщенная модель вейвлет-преобразователя
Генератор сигнала (в данном случае используется генератор синусоидальных сигналов) формирует "оцифрованный" синусоидальный сигнал с заданными величинами амплитуды, частоты и периода дискретизации, который затем поступает на вход "Вейвлет-преобразователя". Вейвлет-преобразователь имеет один вход и два выхода, на первом из которых в соответствии с предварительно заданными условиями формируется сдвинутый во времени сигнал, а на втором - коэффициенты вейвлет-преобразования. Последние, а именно коэффициенты, записываются в файл wavelet.mat, а генерируемый сигнал - в файл data.mat. Одновременно с этим данные, содержащие коэффициенты вейвлет-преобразования поступают также на блок, осуществляющий отображение вейвлет-образа в квазиреальном времени.
Структура модели.
Блок "Вейвлет-преобразователь" выполняет обработку сигнала на шестидесяти четырёх временных масштабах (рис. 3а, б), в соответствии с чем, подаваемый на вход блока сигнал разветвляется на 64 линии и затем, значения коэффициентов вейвлет-преобразования, поступают на вход буфера в виде вектора размером [1x64].
 Рис.3 Структура вейвлет-преобразователя
На выходе буфера в этом случае образуется матрица [64x64], которая подвергается транспонированию в следующем блоке, с возможностью просмотра в квазиреальном времени получаемого на его выходе вейвлет-образа. Для обеспечения синхронизации преобразования, перед разветвлением введен блок, выполняющий дискретизацию сигнала с заданной частотой и блок автоматического переключения, отключающий сигнал, по прошествии заданного количества отсчётов. При этом временная привязка обеспечивается подачей каждого из разветвлённых сигналов на соответствующий блок задержки (рис. 4), состоящий из блоков 'Transport Delay' и дискретизатора. В зависимости от типа вейвлета и временного масштаба, сигнал в этих блоках задерживается на необходимую величину и затем поступает на блок 'Buffer', на выходе которого образуется вектор с количеством элементов, зависящим от выбора типа вейвлета и масштаба.
 Рис.4 Блок "Задержка сигнала"
Сформированный таким образом вектор поступает на вход блока 'Dot Product', на второй вход которого подается равный по размеру вектор постоянных значений вейвлета из блока 'Constant'. Блок 'Dot Product' осуществляет поэлементное умножение векторов с последующим суммированием полученных значений коэффициентов вейвлет-преобразования (рис. 5).
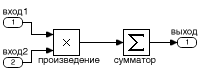 Рис.5 Блок "Dot Product"
Для нормализации полученных коэффициентов, они вводятся в подключенный к выходу блока 'Dot Product' блок 'Задержка сигнала' и, затем, в блок 'Gain'. После нормализации, полученные 64 коэффициента, объединяются с помощью блока 'Mux' в вектор и поступают на выход 'Вейвлет-преобразователя' - блок отображения вейвлет-образа преобразуемого сигнала (рис. 6) с тем же временным масштабом, который был в начале процесса.
Как следует из вышеизложенного, рассмотренная модель является дискретной с априори заданной частотой дискретизации, поэтому продолжительность преобразования зависит от длительности сигнала и выбранного вейвлета.
 Рис.6 Блок отображения вейвлет-образа
Таким образом, если взять ветвь сигнала, соответствующую масштабу a при количестве отсчётов, необходимом для задания минимального вейвлета равном b и частоте дискретизации равной c, размер вектора, содержащего значения вейвлета будет равен [1 x a*b]. В этом случае буфер будет накапливать a*b значений, а (a*b-1) значение будет всегда оставаться постоянным. Задавая во всех дискретизаторах частоту дискретизации равной c, а коэффициент усиления в блоке 'Gain' равным 1/√a сигнал, проходя через первую задержку, будет задерживаться на время (a-1)*c*b/2, через вторую - на (64-a)*c*b и т. д.
Программная реализация.
При создании данной модели в программе Simulink были использованы блоки из библиотек входящих в комплект поставки данной программы, а именно:
- Генератор синусоидального сигнала (библиотека Simulink/DSP Blockset/DSP Sources)
Задается следующими параметрами:
- Амплитуда.
- Частота.
- Фаза.
- Сигнал: дискретный или непрерывный.
- Комплексный сигнал или нет.
- Метод вычисления.
- Частота дискретизации.
- Количество отсчётов во фрейме.
- В какое положение устанавливать при новом обращении к блоку.
- Вейвлет-преобразователь (библиотека Simulink/Signals & Systems)
Содержит в себе подсистему:
- In (библиотека Simulink/Signals & Systems)
Задается следующими параметрами:
- Номер порта
- Port Dimentions
- Частота дискретизации
- Вид данных
- Вид сигнала
- Out (библиотека Simulink/Signals & Systems)
Задается следующими параметрами:
- Номер порта
- Output when disabled: held, reset.
- Initial Output
- Constant (библиотека Simulink/Sources)
Задается следующими параметрами:
- Buffer (библиотека Simulink / DSP Blockset / Signal Management / Buffers)
Задается следующими параметрами:
- Размер буффера
- Buffer Overlap
- Initial Condition
- Mux (библиотека Simulink/Signals & Systems)
Задается следующими параметрами:
- Gain (библиотека Simulink/Math)
Задается следующими параметрами:
- Dot Product (библиотека Simulink/Math)
- N-Sample Switch (библиотека Simulink / DSP Blockset / Signal Management / Switches & Counters)
Задается следующими параметрами:
- Количество отсчётов
- Частота дискретизации
- Zero-Order Hold (библиотека Simulink/Discrete)
Задается следующими параметрами:
- Задержка Сигнала (библиотека Simulink/Signals & Systems)
Содержит в себе подсистему:
- In (библиотека Simulink/Signals & Systems)
Задается следующими параметрами:
- Номер порта
- Port Dimentions
- Частота дискретизации
- Вид данных
- Вид сигнала
- Out (библиотека Simulink/Signals & Systems)
Задается следующими параметрами:
- Номер порта
- Output when disabled: held, reset.
- Initial Output
- Transport Delay (библиотека Simulink/Continuous)
Задается следующими параметрами:
- Временная задержка
- Начальное входное значение
- Начальный размер буфера
- Zero-Order Hold (библиотека Simulink/Discrete)
Задается следующими параметрами:
- Вейвлет-образ в реальном времени (библиотека Simulink/Signals & Systems)
Содержит в себе подсистему:
- In (библиотека Simulink/Signals & Systems)
Задается следующими параметрами:
- Номер порта
- Port Dimentions
- Частота дискретизации
- Вид данных
- Вид сигнала
- Величина константы
- Buffer (библиотека Simulink / DSP Blockset / Signal Management / Buffers)
Задается следующими параметрами:
- Размер буффера
- Buffer Overlap
- Initial Condition
- Transpose (библиотека Simulink / DSP Blockset / Math Functions /Matrices & Linear Algebra / Matrix Operations)
Задается следующими параметрами:
- Размер буффера
- Buffer Overlap
- Initial Condition
- Matrix Viewer (библиотека Simulink / DSP Blockset / DSP Sinks)
Задается следующими параметрами:
- Image Properties
- Axes Properties
- To file: Сигнал на выходе (библиотека Simulink/Sinks)
Задается следующими параметрами:
- Путь и имя файла
- Название переменной, в которой будут содержаться данные
- Частота дискретизации
- Decimation
Задание параметров используемых в модели блоков осуществляется посредством стандартных окон, которые вызываются для предварительно активизированного мышью блока нажатием клавиш Ctrl-E или посредством меню SimulationParameters.
С целью удобства моделирования внутренний GUI библиотеки Wavelet ToolBox системы Matlab был модифицирован таким образом, чтобы обеспечивалось удобство ввода параметров моделирования и отображения текущего вейвлет образа, линии коэффициентов и имеющих место локальных максимумов.
Моделирование.
В принципе, модификация стандартного GUI непрерывного одномерного преобразования была произведена для того, чтобы иметь удобную возможность сравнивать результаты работы модели со стандартными средствами библиотеки Wavelet ToolBox. При необходимости модель может быть запущена и без использования GUI, путем ручного задания параметров.
Для запуска модели с использованием GUI необходимо запустить Matlab 6.0 и из командной строки задать "wavestart", после чего производится загрузка окна программы и выполняется следующая последовательность действий:
-
В меню 'FileLoad Wavelets' выбирается анализирующая функция (вейвлет), с помощью которой должен быть исследован сигнал (рис. 7).
 Рис.7 Выбор анализирующей функции
-
В меню 'File' выбирается 'Model Simulation', приводящее к появлению окна задания параметров моделирования (рис. 8), в котором задается 'Амплитуда Сигнала', 'Частота сигнала', 'Длительность сигнала в отсчётах', 'Частота дискретизации'.
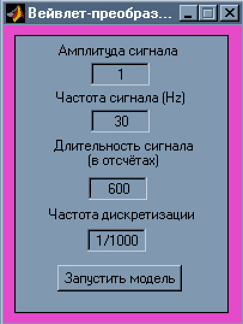 Рис.8 Задание параметров модели
-
В окне задания параметров сигнала, командой 'Запустить модель' открывается окно с моделью вейвлет-преобразователя (рис. 2) и окно, в котором в квазиреальном времени отображается текущий вейвлет-образ (рис. 9).
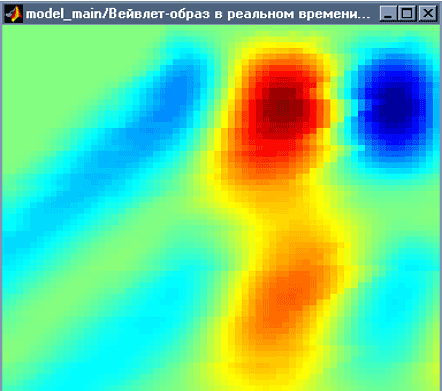 Рис.9 Окно вейвлет-образа сигнала
-
По окончании моделирования, в меню 'File' выбирается команда 'View results', по которой загружается файл 'wavelet_ok.mat' и в исходном окне появляется исследуемый сигнал, его вейвлет-образ, а также линии коэффициентов и локальных максимумов (рис. 10).
 Рис.10 Окно результатов вейвлет-преобразования
Здесь следует еще раз отметить, что данная последовательность действий не является обязательной и если пользователь желает произвести только часть действий, например, только запустить модель или посмотреть готовый вейвлет-образ, достаточно загрузить сохраненный исследуемый сигнал, установить необходимые параметры и задать команду "Analize".
Пример использования модели.
Одной из перспективных областей применения данной модели является установление степени искажения сигнала, прошедшего через тот или иной объект телекоммуникаций, в частности, через линию связи. Для этого достаточно установить соответствие входному сигналу refdata реального (искаженного) выходного сигнала degdata , а точнее их вейвлет-образов, полученных с выходов вейвлет-преобразователей (рис. 11).
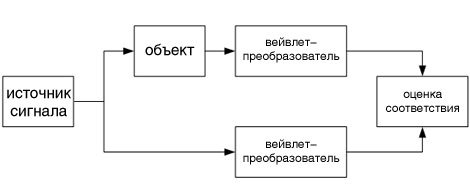 Рис.11 Схема оценки пройденного через объект сигнала
Оценка соответствия [4, 5] здесь включает предобработку входного и выходного сигналов, которая заключается в удалении постоянных составляющих (трендов) refdata= refdata- mean(refdata) и degdata= degdata- mean(degdata), а также в выполнении фильтрации refdata= filter(hinput,refdata), degdata= filter(hinput,degdata) с целью более яркого выделения особенностей данных сигналов. Для правильного сопоставления с входным сигналом, искаженный сигнал помимо этого подвергается удалению задержек различной природы, дополнительной фильтрации и т. д.
По окончании предварительной обработки входного refdata и выходного degdata сигналов выполняется их вейвлет-преобразование с установлением соответствия одноименных вейвлет-образов Refsurf[ω,t] и Degsurf[ω,t], которые представляются в боле значимом трёхмерном виде, позволяющем провести оценку различия сигналов по трём характеристикам: времени, частоте и амплитуде. Этот факт является определяющим и отличает такую оценку от традиционного способа, позволяя оперировать не только со всем сигналом, но с наиболее существенными его участками, тем самым, более экономно устанавливая степень соответствия при той же эффективности. На основе проведённого таким образом сравнения, накапливается полная информация обо всех возникающих отклонениях, на основе которой формируется заключение о соответствии
Errsurf[ω,t]=Degsurf[ω,t]-Refsurf[ω,t], где ω - частота, t - время.
Заключение.
Рассмотренная модель квазиреального во времени вейвлет-преобразователя может служить основой для проектирования вейвлет-анализаторов онлайновых сигналов, а также для имитационного моделирования процессов телекоммуникаций, вводя в качестве исследуемого объекта блоки из Telecommunication Toolbox системы Matlab или создавая свои модели таких блоков. В настоящее время специалистами компании SYRUS SYSTEMS реализована система квазиреального во времени вейвлет-преобразования для анализа сигналов с частотой дискретизации до 100 МГц.
Литература
- Jaideva C. Goswami, Andrew K. Chan. Fundamentals of Wavelets: theory, algorithms, and applications. A Wiley-Interscience Publication, 1999, 306р.
- Добеши И. Десять лекций по вейвлетам, перевод. - Ижевск: НИЦ "Регулярная и хаотическая динамика", 2001, 464с.
- Н.М. Астафьева, Вейвлет-анализ: основы теории и примеры применения, Успехи Физических Наук, 166 (11), (1996) 1145р.
- Иванов А. Н. Контроль качества инфокоммуникаций с использованием вейвлет-анализа. Метрология и измерительная техника в связи, 1, 2003, с. 33-35.
- Иванов А. Б. Контроль соответствия в телекоммуникациях и связи: Измерения, анализ, тестирование, мониторинг. - М.: Компания Сайрус Системс. 2000, 375 с.
|


